반응형

ML Evaluation Metric
머신러닝에서는 학습이 잘 되었는지 확인하기 위한 다양한 Metric이 존재한다.
대표적인 Metric들을 알아보자.
Classification(분류) Metric
Confusion Matrix(오차 행렬)

- 기준은 Model이 낸 output이 기준이 되므로, Prediction을 기준으로 명명한다.
- 모델이 Positive로 분류했으면 Positive, 모델이 Negative로 분류했으면 Negative로 명명된다.
- 이 때, 정답을 맞춘 Positive라면 True Positive(TP), 정답을 틀린 Positive라면 False Positive(FP)가 되는식이다.
- 위에서 표시된 TP, FP, FN, TN을 바탕으로 다양한 Metric을 구할 수 있다.
- Accuracy
- TP + TN / (TP+FP+TN+FN)
- 전체중에 True의 개수 - Precision(정밀도)
- TP / (TP + FP)
- 모델이 예측한 positive중에서 실제 Positive의 비율 - Recall (재현율)
- TP / (TP + FN)
- 실제 Positive중 모델이 예측한 비율 - Fall-Out
- FP / (FP + TN)
- 실제로는 Negative인데 모델이 Positive로 오탐한 비율 - F1 Score
- 무조건 Positive로 분류하면 Recall이 1이 되지만 Precision이 폭락하고, 무조건 Negative로 분류하면 Precision은 1이 되지만 Recall이 0이 된다.
- 이처럼 Precision이나 Recall은 단일 Metric으로 사용하기엔 모델의 일반화 성능을 나타낼 수 없다는 한계점이 존재하기 때문에 Precision 과 Recall의 조화평균값인 F1 Score를 사용할 수 있다.
- Receiver Operation Characteristic Curve(ROC) - Area Under Curve(AUC)

출처: https://glassboxmedicine.com/2019/02/23/measuring-performance-auc-auroc/
- 통칭 ROC-AUC
- Fall out과 Recall을 통해 FPR, TPR을 X,Y축으로 두고 Threshold를 변경시키면서 그린 곡선을 ROC라고 한다.
- 이 때, ROC를 수치화 할 수 있는 방법이 딱히 없으므로, Area Under Curve라는 곡선 밑 부분의 넓이 값을 통해 성능을 측정한다. Recall이 높고, Fall Out은 낮을 수록 넓이가 1에 가까워진다.
Regression(회귀) Metrics
- MAE(Mean Absolute Error)
- 예측값과 Ground Truth 사이의 차이의 절대값의 평균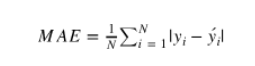
- MSE(Mean Squared Error)
- 예측값과 Ground Truth 사이의 차이의 제곱의 평균
- 제곱 때문에 Anomaly Data에 매우 민감함(크기가 어마어마하게 커질 수 있음)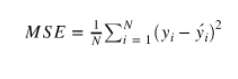
- RMSE(Root Mean Squared Error)
- MSE에 루트를 씌운 값
- Anomaly에 상대적으로 덜 민감함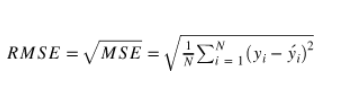
- RMSLE(Root Mean Squared Logarithmic Error)
- 예측값과 정답값에 로그를 취한 뒤 계산한 RMSE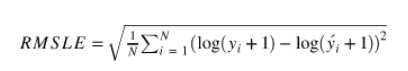
반응형
'Machine Learning > ML기초' 카테고리의 다른 글
| [ML 이론] Feature Normalization, SoftMax (0) | 2021.12.20 |
|---|---|
| [ML 수학] Kullback Leibler Divergence(KL Divergence, Cross Entropy) (0) | 2021.12.16 |



