[ML 수학] Kullback Leibler Divergence(KL Divergence, Cross Entropy)

---

Kullback Leibler Divergence(KL Divergence)

DeiT 논문을 분석하다보니 Kullback Leibler Divergence(쿨백-라이블러 발산) 개념이 나왔는데, 전에도 Autoencoder를 공부하면서 봤었던 내용인데 이참에 제대로 정리를 하고자 포스팅을 작성하게 되었다. 정리를 안해두니까 매번 볼 때마다 새롭다. 내 기억력....

 

Kullback Leibler Divergence란 기본적으로 두 개의 서로 다른 확률 분포를 비교하는 방법이다.

관찰된 데이터 혹은 복잡한 데이터 분포를 이를 나타낼 수 있는 확률 통계 모델로 나타내었을 때, 이러한 모델이 실제 관측치 대비 얼마나 정보를 잃어버렸는지 측정한다.

 

잘 정리된 외국 블로그의 예시를 참고해보자
(https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained)

 

 

우리는 우주에 나와서 실험을 진행하고 있는 과학자들이다.
우리의 주 연구과제는, 외계행성에 존재하는 우주벌레에 관한 연구이다.
각 벌레들은 10개의 이빨을 가질 수 있으나, 음식을 씹는등 살아가는 과정에서 벌레들은 이빨을 잃기도 한다.
벌레들의 이빨의 분포를 충분히 많은 관찰을 통해 다음과 같이 얻어냈다.

 

 

이를 이대로 지구로 전송해도 되겠지만, 

우리는 연구자가 아닌가! 이빨의 개수를 잘 나타낼 수 있는 확률 모델을 만들어 지구로 전송해야 한다.

 

먼저 이를 Uniform Appoximation을 통해 나타내면 다음과 같다.

이빨이 존재할 수 있는 경우의 수 0개~ 10개 까지의 11가지의 경우의수의 확률이 약 9%로 동일하다고 가정한다.

 

 

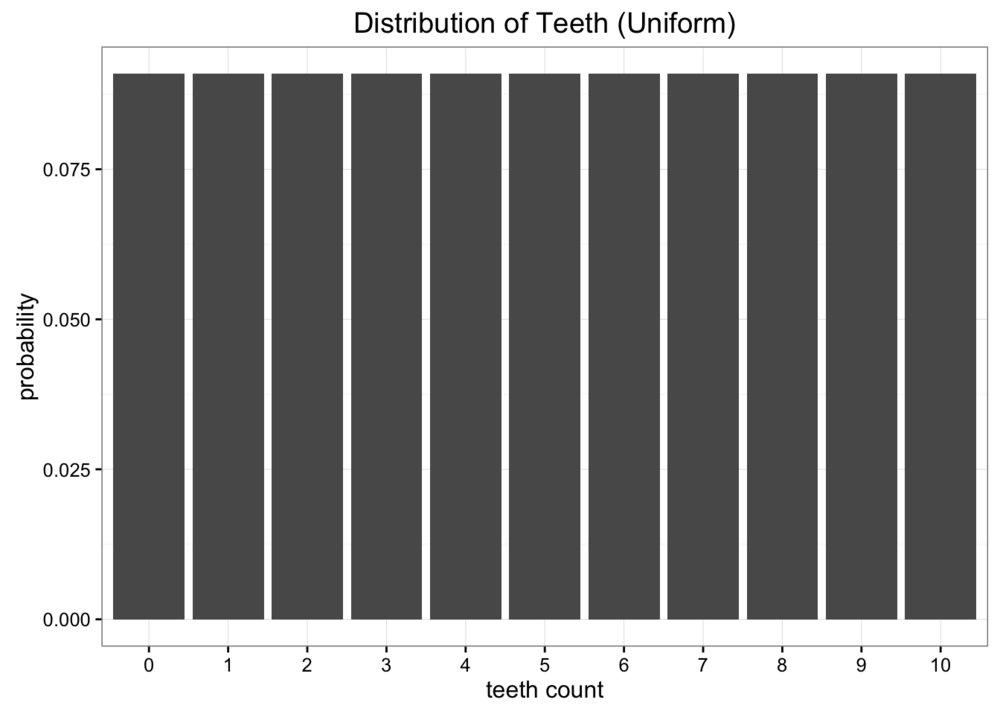
둘째로는, 이빨의 평균 개수가 5.7개라는 정보를 미리 알고 있다면 이를 Binomial Approximation을 통해 표현할 수 있다.

n이 10, p가 x일 때, 10x = 5.7이므로 확률 p는 0.57과 같고, 이를 통해 이항 분포로 그려내보자.

 

 

 

얼핏 보기엔, 균등 분포보다 훨씬 좋아보인다. 이제 값들을 실제 관측값과 비교해보자.

 

 

각각의 모델들이 실제 관측값 대비 얼마나 정보가 손실되었는지 객관적으로 확인할 수 있다면, 

어떤 분포 모델이 가장 적합한지 수치화하여 표현할 수 있을 것이다. 

이 때, 사용되는 개념이 ML을 하다보면 흔히 알게 되는 Entropy이다.

 

 

Entropy

---

Entropy에서 만약 log2를 사용하게 된다면, 이 값을 통해 데이터가 가진 정보량을 나타내는데에 필요한 최소한의 Bit 수를 알 수 있게 된다. 물론 Entropy 자체에서 어떻게 해야 데이터가 가진 정보를 최적화해서 Encoding할 수 있는지에 대한 사항은 알 수가 없다. 단지 정보를 나타낼 때 필요한 최소한의 Bit 수를 알 수 있다는것에 의의가 있다.

 

즉, Entropy 개념을 사용하면 데이터에 담긴 정보량을 객관적으로 수치화할 수 있으며, 이를 각각의 확률 분포 모델에 적용한 뒤 비교하면 각 모델들이 얼마나 정보를 소실하는지 알아낼 수 있는 것이다.

 

 

 

 

KL Divergence

---

 

KL Divergence는 결국 실제 확률 분포 p에 대한 log값과 q에 대한 log값의 차이에 대한 entropy를 구하는 것과 같다.

이를 통해 실 관측값과 추측 모델간에 발생하는 정보량의 소실을 알아낼 수 있다. 

 

그리고, 이를 전개해보면 꽤나 익숙한 모양의 식이 나타나는데, 

 

 

결국 해당 값은 p와 q의 Cross Entropy에서, Entropy(p)를 뺀 것과 같다는 것을 확인할 수 있다.

이 때, Entropy(p)는 결국 상수값이므로, KL Divergence를 최소화시키기 위해서는 결국 Cross Entropy를 최소화시켜야 한다.

 

이 개념이 바로 딥러닝에서 사용되는 Cross Entropy Loss이다.

특정 Parameter에 대해 미분하면서 Backpropagation을 수행하는 Neural Network의 구조상, 어차피 Parameter와 관련이 없는 Entropy, H(p)는 결국 상수처리되어 미분시 사라져버린다. 따라서 결국 Cross Entropy를 최소화 하는 방향으로 학습이 진행되게 된다.

 

 

 

Result

---

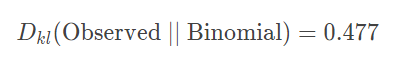
KL Divergence로 확인한 결과, Uniform이 Binomial 방식보다 정보의 손실이 적다는 것이 나타났다.

따라서, 우주벌레의 이빨의 개수를 더 잘 나타내는 확률분포는 이항 분포가 아닌 균등 분포라는 것을 확인할 수 있다.

 

이 때, 한가지 유의해야 할 점은 KL Divergence는 대칭구조가 아니므로, Distance의 개념이 아니다.

즉, p에 대한 q의 KL Divergence와 q에 대한 p의 KL Divergence는 아래와 같이 값이 완전히 달라진다.

 

 

여기까지, KL Divergence에 대해 알아보았다.

딥러닝에서 CE Loss를 통해 학습시킬 때, KL Divergence 개념이 들어가 있었다는 것은 이번에 정리를 하면서 깨닫게 되었다. 역시 딥러닝은 수학적으로 공부해야할 것이 끝도 없는 것 같다.