
백준 - 단계별로 풀어보기 [1002]
https://www.acmicpc.net/problem/1002
문제

A라는 사람의 좌표 x1,y1과 B라는 사람의 좌표 x2,y2 그리고 임의의 좌표 C에 대하여 A로부터의 거리 r1와 B로부터의 거리 r2를 입력받았을 때 존재할 수 있는 C의 개수를 출력하는 문제이다.
풀이
이 문제는 사실 중학교 수학을 알아야 풀 수 있는 내용이다.
원의 정의란, 한 점에서 일정한 거리만큼 떨어진 점들의 집합이다.
따라서 A좌표에서 거리가 r1일 수 있는 C들의 집합은 A좌표를 중심으로하고 반지름이 r1인 원의 형태를 가지고 있으며,
B좌표에서 거리가 r2일 수 있는 C들의 집합은 B좌표를 중심으로 하고 반지름이 r2인 원의 형태를 가지고 있다.
즉 이때, 존재할 수 있는 C들의 개수는 이러한 두 원의 접점의 개수를 의미한다.
위와 같은 접근에서 알 수 있는 사실은 두 점 사이의 거리의 따라 답이 결정된다는 것이다.
가능한 경우의 수는 다음과 같다.
d = r1 + r2 일 때, 두 원은 접하고 있으므로 가능한 C는 1개

r1 - r2 < d < r1 + r2 일 경우, 두 원은 두 점에서 접하므로 가능한 C는 2개
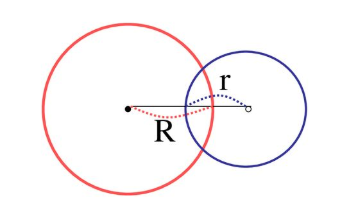
그 외의 경우에는 접하지 않으므로 가능한 C는 0개이다.
코드
#include <iostream>
using namespace std;
int main() {
int x1,y1,r1,x2,y2,r2,d,cond1,cond2,num;
cin >> num;
for(int i = 0; i < num; i++)
{
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
d = (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2);
cond1 = (r1-r2) * (r1-r2);
cond2 = (r1+r2) * (r1+r2);
if(d == 0)
{
if(cond1 == 0)
cout << "-1" << '\n';
else
cout << "0" << '\n';
}
else if (d == cond1 || d == cond2)
cout << "1" << '\n';
else if (cond1 < d && d < cond2)
cout << "2" << '\n';
else
cout << "0" << '\n';
}
}평가
두 원의 위치관계에 대한 개념을 깨닫고 풀 경우 쉽게 풀 수 있으나, 이를 생각하지 못하면 다소 풀이가 막막한 문제이다.
정답률은 19.474%로 매우 어려운 문제로 분류된다.
'Algorithm > Baekjoon BOJ' 카테고리의 다른 글
| [백준 / BOJ] - 10870번 피보나치 수 5 C++ 풀이 (0) | 2020.02.26 |
|---|---|
| [백준 / BOJ] - 10872번 팩토리얼 C++ 풀이 (0) | 2020.02.26 |
| [백준 / BOJ] - 3053번 택시 기하학 C++ 풀이 (0) | 2020.02.25 |
| [백준 / BOJ] - 4153번 직각삼각형 C++ 풀이 (0) | 2020.02.18 |
| [백준 / BOJ] - 3009번 네 번째 점 C++ 풀이 (0) | 2020.02.18 |



